게임 개발 낙서장

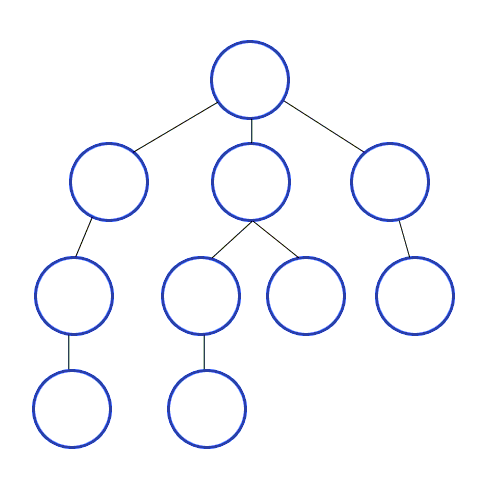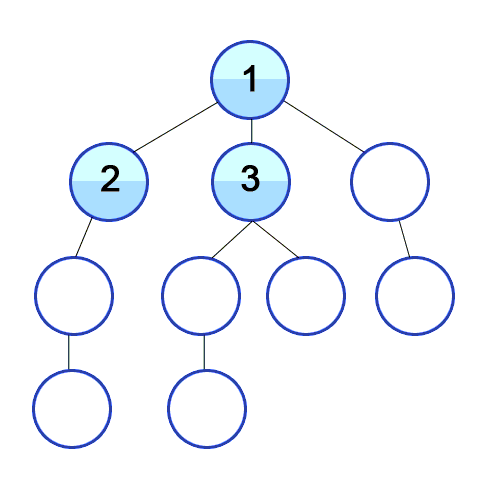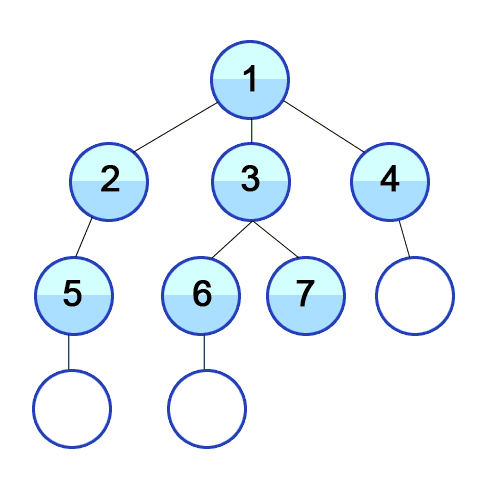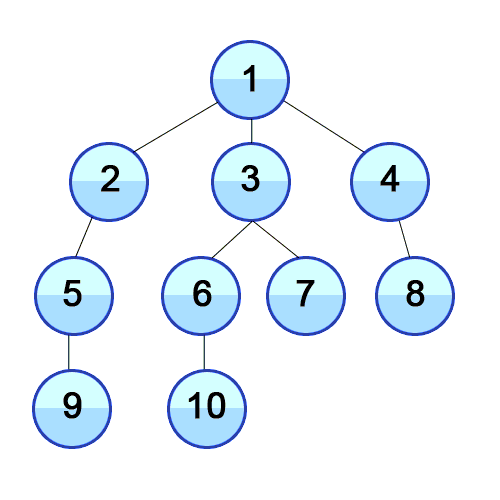
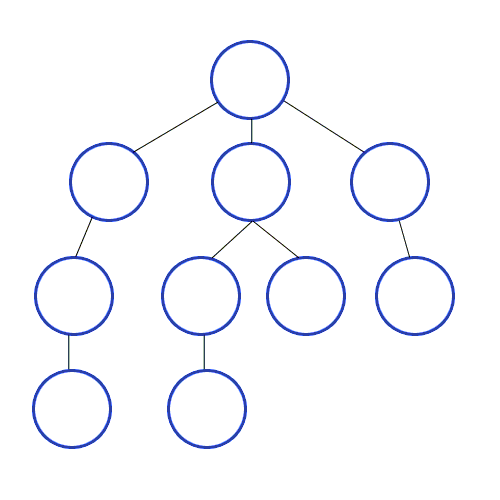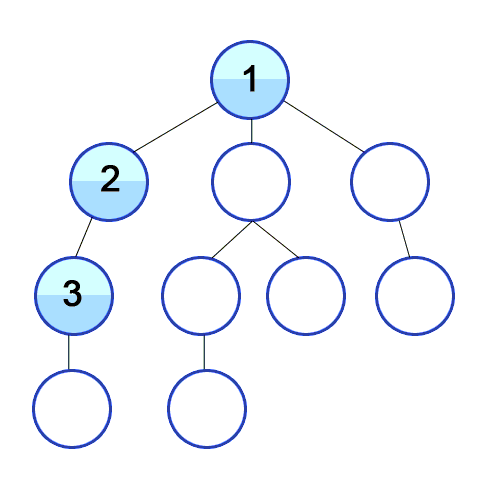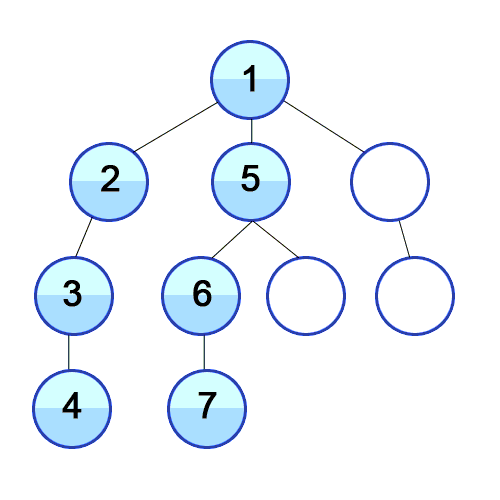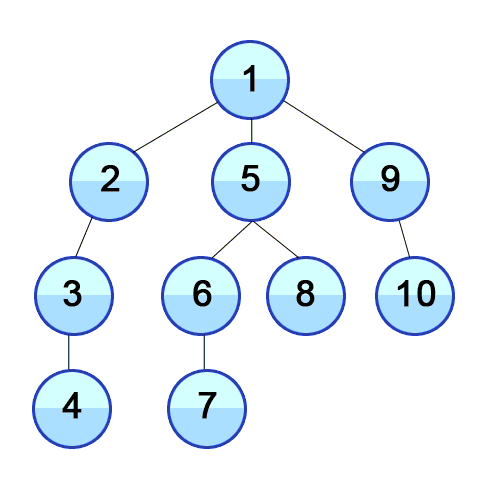
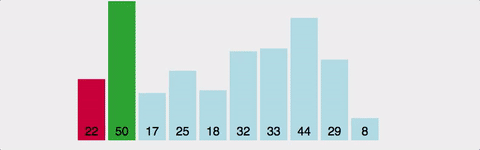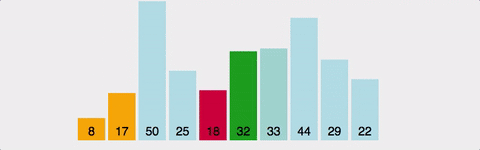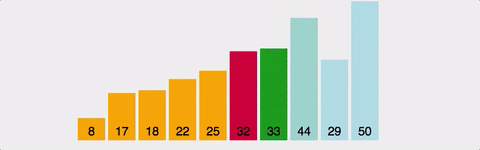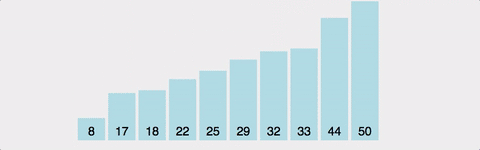
개념 하나의 정점으로부터 시작하여 인접한 노드를 모두 방문하고 차례대로 모든 정점들을 한 번씩 방문하는 알고리즘 과정 장점 장점으로는, 출발노드에서 목표노드까지의 최단 길이 경로를 보장합니다. (물론 모든 간선의 가중치가 동일할 경우입니다.) 단점 단점으로는, 최악의 경우 모든 노드에 대한 정보를 위한 공간을 요구한다는 것입니다. 따라서 최대 저장공간을 크게 잡아야 합니다. 또한 목표노드가 깊은 단계에 있을 경우 오랜 시간이 소요됩니다. 시간복잡도 인접 행렬 : O(V^2) 인접 리스트 : O(V+E) 소스코드 - 인접리스트 public class BreadthFirstSearch_Source : MonoBehaviour { void Start() { int n = 5; // 정점의 개수 int m = ..

개념 BFS와는 다르게 루트 노드 혹은 임의의 노드와 인접한 노드를 모두 탐색하는 것이 아니라, 연결된 정점들을 차례대로 한번씩 방문하는 알고리즘이다. 즉, 이름과 같이 넓게 탐색하기 이전에 깊게 탐색하는 알고리즘이다. 과정 장점 장점으로는, 현 경로상의 노드들만 기억하면 되므로 그래프의 높이 만큼의 공간만을 요구합니다. 따라서 최대 저장공간의 수요가 비교적 적습니다. 또한, 목표노드가 깊은 단계에 있을 경우에 해를 빠르게 구할 수 있습니다. 단점 단점으로는, 해가 없는 경로에 깊이 빠질 가능성이 있다는 것입니다. 또한 얻어진 해가 최단 경로가 된다는 보장이 없습니다. (목표에 이르는 경로가 다수인 문제에 대해 깊이우선 탐색은 해에 다다르면 탐색을 끝내버리므로, 이 때 얻어진 해는 최적의 해가 아닐 수 ..

개념 이진 탐색이란 데이터가 정렬돼 있는 배열에서 특정한 값을 찾아내는 알고리즘이다. 배열의 중간에 있는 임의의 값을 선택하여 찾고자 하는 값 X와 비교한다. X가 중간 값보다 작으면 중간 값을 기준으로 좌측의 데이터들을 대상으로, X가 중간값보다 크면 배열의 우측을 대상으로 다시 탐색한다. 동일한 방법으로 다시 중간의 값을 임의로 선택하고 비교한다. 해당 값을 찾을 때까지 이 과정을 반복한다. 과정 오름차순으로 정렬된 배열이 있다. { 17, 28, 43, 67, 88, 92, 100 } 이 배열에서 이진 탐색을 이용하여 43의 값을 찾아보자. 첫 번째 시도 우선 가운데에 위치한 임의의 값 67을 선택한다. 선택한 값 67과 찾고자 하는 값 43를 비교한다. 43 < 67 이므로 43은 67의 좌측에 ..

개념 Insertion Sort는 Selection Sort와 유사하지만, 좀 더 효율적인 정렬 알고리즘이다. Insertion Sort는 2번째 원소부터 시작하여 그 앞(왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입 하여 정렬하는 알고리즘이다. 최선의 경우 O(N)이라는 엄청나게 빠른 효율성을 가지고 있어, 다른 정렬 알고리즘의 일부로 사용될 만큼 좋은 정렬 알고리즘이다. 과정 정렬은 2번째 위치(index)의 값을 temp에 저장한다. temp와 이전에 있는 원소들과 비교하며 삽입해나간다. '1'번으로 돌아가 다음 위치(index)의 값을 temp에 저장하고, 반복한다. 시간복잡도 최악의 경우(역으로 정렬되어 있을 경우) Selection Sort..

개념 Selection Sort는 Bubble Sort과 유사한 알고리즘으로, 해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘이다. 과정 주어진 배열 중에 최소값을 찾는다. 그 값을 맨 앞에 위치한 값과 교체한다. (pass) 맨 처음 위치를 뺀 나머지 배열을 같은 방법으로 교체한다. 시간복잡도 데이터의 개수가 n개라고 했을 때, 첫 번째 회전에서의 비교횟수 : 1 ~ (n-1) => n-1 두 번째 회전에서의 비교횟수 : 2 ~ (n-1) => n-2 ... (n-1) + (n-2) + .... + 2 + 1 => n(n-1)/2 비교하는 것이 상수 시간에 이루어진다는 가정 아래, n개의 주어진 배열을 정렬하는데 O(n^2) 만큼의 시간이 걸린다. 최선, 평균,..

개념 Bubble Sort는 Selection Sort와 유사한 알고리즘으로 서로 인접한 두 원소의 대소를 비교하고, 조건에 맞지 않다면 자리를 교환하며 정렬하는 알고리즘 이다. 과정 1회전에 첫 번째 원소와 두 번째 원소를, 두 번째 원소와 세 번째 원소를, 세 번째 원소와 네 번째 원소를, … 이런 식으로 (마지막-1)번째 원소와 마지막 원소를 비교하여 조건에 맞지 않는다면 서로 교환한다. 1회전을 수행하고 나면 가장 큰 원소가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 원소는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 원소까지는 정렬에서 제외된다. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다. 시간복잡도 주어진 배열 안에서 교환(swap)을 통해..

문제 풀이 전 이론 - 1 - 2보다 큰 모든 짝수는 두 소수의 합으로 표현 가능하다 - 위의 문장에 3을 더하면 - 5보다 큰 모든 홀수는 세 소수의 합으로 표현 가능하다로 바뀐다. - 이는 아직 증명되지 않은 문제이기 때문에 "추측"이다. - 하지만 $10^18$이하에서는 참인 것이 증명되었기 때문에, 알고리즘 문제를 푸는데에는 전혀 문제가 없다. 문제 풀이 - 이 문제는 n의 최악의 경우가 100만이고, 테스트 케이스 문제이기 때문에 - 크기가 100만인 배열을 할당하여 미리 정답을 저장해놓고, 반복문을 통하여 입출력을 해야한다. - 입력은 짝수를 받으며, 짝수 = 홀수(소수) + 홀수(소수)이므로, 소수들을 미리 배열에 저장해놓는 방법을 사용한다. - 일단, 에라토스테네스의 체를 이용하여 100만..

문제 풀이 전 이론 - 1 - 해당 문제는 소수 찾기1과 동일하지만, 입력에서 최악의 경우가 실행 시간에 치명적인 영향을 미친다. - 기존의 방법으로 풀었으면 약수를 알아내는 시간 O($\sqrt{N}$)과 모든 N에 대한 O(N)로 인해 O(N$\sqrt{N}$)이 될 것이다. - 일단 최악의 경우가 백만이라고 하면 의심해봐야 한다...(꿀팁) - 이에 대한 문제를 효율적으로 해결할 수 있는 방법은 에라토스테네스의 체 알고리즘을 사용하는 것이다. 문제 풀이 전 이론 - 에라토스테네스의 체 - 1부터 N까지 범위 안에 들어가는 모든 소수를 구하려면 에라토스테네스의 체를 사용한다. - 이를 이용하면 N이 100만인 경우 + 테스트케이스 문제일 때, 모든 소수를 크기가 100만인 배열에 미리 저장해놓고, 입..

문제 풀이 전 이론 - 1 - 소수는 약수가 1과 자기 자신 밖에 없는 수이다. - N이 소수이기 위해서는 N/(2-(N-1))이 0으로 나누어 떨어져서는 안된다. - 소수를 구하는 방법은 두가지가 있다. - 1. 어떤 수 N이 소수인지 아닌지를 판별한다.(효율성을 크게 안따져도 되는 경우) - 2. N이하의 모든 소수를 다 구한다.(N의 맥시멈이 100만이어서 미리 저장해놓아야 하는 경우) - 해당 문제는 N의 최악의 경우가 치명적이지 않으므로 첫 번째 방법을 사용해보겠다. 문제 풀이 전 이론 - 2 - 어떤 수 N이 소수인지 아닌지를 판별하기 위해서는 N을 2~N-1로 나누었을 때 0이 나오는지 살펴보면 된다. - 하지만, 굳이 N-1까지 반복해볼 필요도 없다. 약수 파트에서 살펴보았듯이 약수는 대칭..

문제 풀이 전 이론 - 1 - 최대공약수는 줄여서 GCD라고 한다. - 두 수 A와 B의 최대공약수 G는 A와 B의 공통된 약수 중에서 가장 큰 정수이다. - 최대공약수를 구하는 가장 쉬운 방법은 2부터 min(A,B)까지 모든 정수로 나누어 보는 방법이 있다. - min(A,B)인 이유는 어차피 두 수의 공통된 약수 중 가장 큰 정수는 min(A,B)보다 크지 않기 때문이다. - 위의 이론은 O(N)이고, 입력이 10,000이하이기 때문에 시간 제한 1초 내에는 충분히 실행가능하다. - 하지만 이보다 더 빠른 방법으로 문제를 해결하기 위해 유클리드 호제법]을 사용해본다. int g =1; for(int i = 2; i